最近在开发一个流程化建模的功能，即用户将多个算子的输入输出连接起来构成流程图，完成建模并执行。其中涉及到一个重要的技术过程，是将算子按照输入输出的依赖关系进行排序，对于任意一个算子，其依赖的前驱算子都排在前面，保证算子执行的时候输入条件已准备好。

实际上，上面构建的流程化模型是一个有向无环图（Directed Acyclic Graph, DAG）。顾名思义，DAG有三大特点：“有向”、“无环”、“图”。DAG首先是一种“图”，这种“图”是有方向性的，并且没有环路。

DAG是一个专业术语，虽然对于一般人比较陌生，但它实际上隐藏在生活中的方方面面。例如，一个工程项目有多个子项目组成，子项目之间有先后关系，一个子项目的开展必须保证前面的项目完成；工厂里面生产的产品，产品由若干部件组成，每个部件再由多个零件组成，组装时必须保证一定的先后顺序。在软件领域，我们也会不知不觉地碰到DAG，例如程序模块之间的依赖关系、makefile脚本、区块链、git分支等。

按照依赖关系对DAG的顶点进行排序，使得对每一条有向边(u, v)，均有u（在排序记录中）比v先出现，这种排序就是拓扑排序。

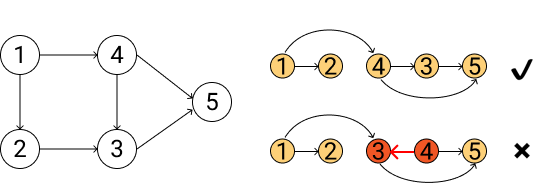
例如，下图中1 → 2 → 4 → 3 → 5是一个正确的拓扑排序，每个节点都在它说依赖的节点后面。而1 → 2 → 3 → 4 → 5则不满足拓扑排序的要求，3依赖于4却出现在前面。

基本原理

对于有向图进行拓扑排序要解决两个问题：一是要判断待排序的有向图是不是无环；二是按照依赖关系生成正确的序列。

我们可以从入度着手，选择一个入度为0的节点，说明该节点不依赖于其他节点，可以放在结果序列最前面。然后，删除该节点和节点的边，找出下一个入度为0的节点，依次放到结果序列中。重复以上过程，即可完成拓扑排序。这种方法可称之为入度方法。

同样，我们也可以从出度着手，选择一个出度为0的节点，说明没有任何节点依赖该节点，可以放到结果序列最末尾。然后，删除该节点和节点的边，找出下一个出度为0的节点，依次放到结果序列尾部。重复以上过程，即可完成拓扑排序。这种方法可称之为出度方法。

不管是入度方法还是出度方法，如果最后还存在入（出）度不为0的节点，或者结果序列中的节点个数不等于有向图中的节点个数，说明有向图中存在环。

按照维基百科的说法，拓扑排序主要有Kahn算法和DFS（深度优先搜索）算法两种。Kahn算法采用入度方法，以循环迭代方法实现；DFS算法采用出度方法，以递归方法实现。Kahn算法和DFS算法的复杂度是一样的，算法过程也是等价的，不分优劣，因为本质上循环迭代 + 栈 = 递归。

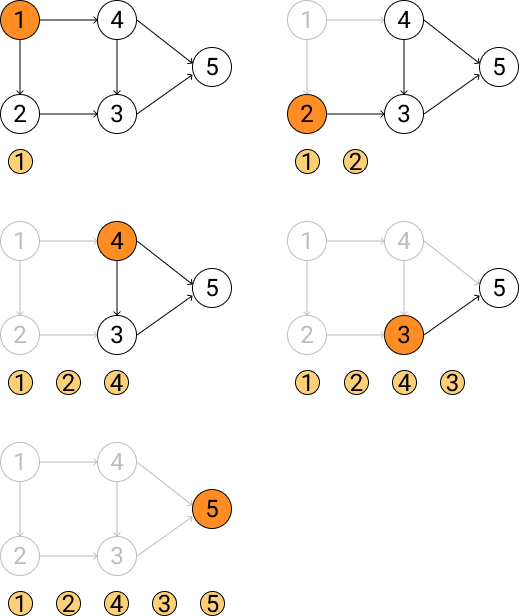
Kahn算法

Kahn算法采用入度方法，其算法过程如下：

  1. 选择入度为0的节点，输出到结果序列中；
  2. 删除该节点以及该节点的边；
  3. 重复执行步骤1和2，直到所有节点输出到结果序列中，完成拓扑排序；如果最后还存在入度不为0的节点，说明有向图中存在环，无法进行拓扑排序。

下图是对Kahn算法的演绎：

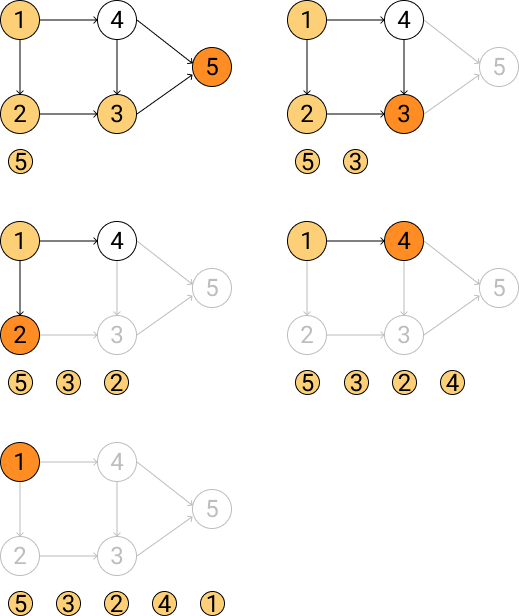
DFS算法

DFS算法采用出度算法，其算法过程如下：

  1. 对有向图进行深度优先搜索；
  2. 在执行深度优先搜索时，若某个顶点不能继续前进，即顶点的出度为0，则将此顶点入栈。
  3. 最后对栈中的序列进行逆排序，即完成拓扑排序；如果深度优先搜索时，碰到已遍历的节点，说明存在环。

下图是对DFS算法的演绎：

One more thing

仔细观察发现，Kahn算法并不一定局限于入度方法，同样适用于出度方法，过程为先选择一个出度为0的节点输出，然后删除该节点和节点的边，重复“选择-删除”过程直到没有出度为0的节点输出，最终序列的逆排序即是拓扑排序结果。这个过程实际上是将原来的有向图的边反向，原来的入度变出度、出度边入度，Kahn算法将出度当成入度处理，最后我们再将结果逆序就还原了拓扑排序结果。

同样，DFS算法也不一定局限于出度算法，我们同样可以将有向图反向，入度变出度、出度边入度。由于我们对有向图反向，所以需要对结果做两次逆序操作，两次逆序操作相当于不需要逆序操作，所以结果序列刚好是拓扑排序结果。

最后，我将在下篇文章中使用Javascript来分别实现Kahn算法和DFS算法。

参考文献

Topological sorting
有向无环图的拓扑排序
浅谈什么是图拓扑排序