在制图过程中，对多边形进行标注是一个常见的需求。然而如何快速找到一个合适的注记点，确不是一个很容易的事情。

最近，Leaflet的作者Vladimir Agafonkin大神发表了一篇博文，描述了他如何用100多行JS代码，实现一个高效的多边形标注点搜寻算法。

虽然他在博文中描述了算法的原理，但是对于我这种数学不好的人，有些细节方面的东西还不甚了解。因此，此篇文章将以我这种小白角度，事无巨细地解释下他的算法。

问题描述

对于一个多边形，哪一个点才适合做标注点呢？自然而然我们就会想到是重心，即centroid。然而对于凹多边形或者环，它们的重心会出现在多边形外部，这明显不是我们想要的。

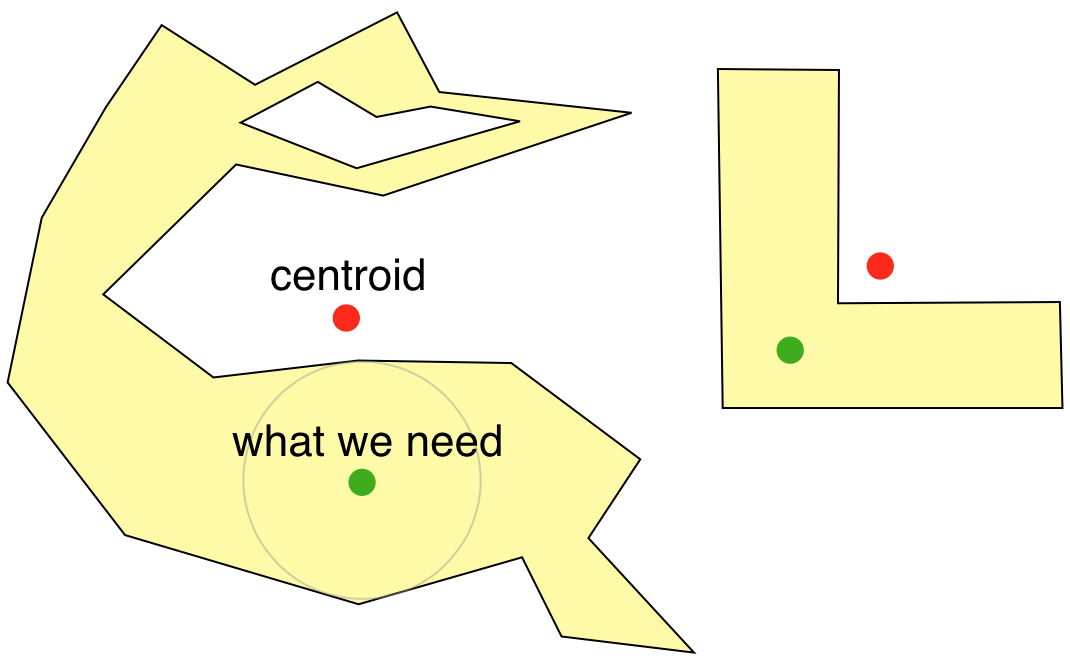
一个合适的标注点，应该是多边形的视觉中心，即以该点为圆心在多边形内部画一个圆，该圆的面积是最大的。假如我们定义一个点到多边形的距离为该点到多边形各边的最短距离，并且规定点在多边形内部时距离为正，点在外部时距离为负。所以多边形标注问题就可以简化为寻找离多边形最远的点，即pole of inaccessibility。

算法原理

理论上，只要知道多边形的各点坐标，必定能够用数学公式求出这个离多边形最远的点。然而，求解这个标注点的精确坐标必定非常耗时，实际上我们只需要一个近似解就足够了。

如何搜寻这个点呢？其实算法原理很简单，即利用分而治之的思想，先搜寻一小块区域的pole of inaccessibility，逐步淘汰差的区域，逐步缩小搜寻范围，最终找到最优点。具体步骤为：

  1. 对多边形进行格网划分，求出格网内部的点到多边形的可能的最大距离。
  2. 按可能的最大距离对格网进行排序，淘汰距离小的格网，保留距离大的格网。
  3. 对剩下的格网再进行细分，重复步骤1和步骤2。

在以上的步骤中，如何计算格网内部的点到多边形可能的最大距离是一个问题。如下图，格网中心点到多边形的距离为dist，到顶点的距为radius，那么格网到多边形可能的最大距离maxd = dist + radius。

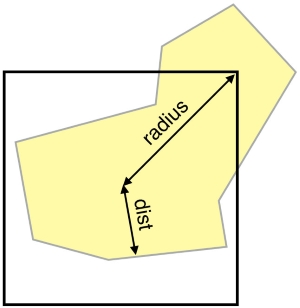
如何证明上述计算最大距离的公式呢？我几何学得不好，没办法给出严密的数学证明，但是我可以通过图示予以说明。

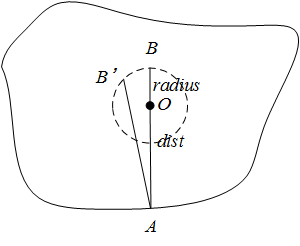
如下图，设多边形内部一点O，其距多边形的距离OA长度为dist。以O为圆心，以radius为半径作一个圆。延长AO，交圆于点B，那么AB的长度为dist + radius。在圆内部任意取一点B'，显然AB' <= AB = dist + radius。假设点B‘到多边形的距离为d，那么d <= AB' <= AB = dist + radius。所以对于圆内的任意一点，其到多边形的距离必定小于等于dist + radius。在圆内部取一个正方形区域，仍然符合d <= dist + radius，这就证明格网区域的最大距离为dist + radius。

如何对格网进行细分呢？我们可以用四叉树，将一个格网分割为4个小格网。

搜寻标注点的算法原理是不是很简单？我将在下一篇博文中详细描述如何用JS实现该算法。