在上一篇博文中，我讲了多边形注记点搜索算法的基本原理，本篇文章讲一讲如何用JS实现。

建议读者阅读本篇博文之前，一定要先了解上一篇博文中提到的算法原理。

函数接口

我们定义一个函数接口，接受一个多边形，计算其标注点：

1
2
3
4
5
6
function polylabel(polygon) {
  // TODO
  return [x, y]
}

module.export = polylabel

使用时，我们可以这样调用：

1
2
3
4
var polylabel = require('polylabel')

var polygon = [[[0, 0], [0, 1], [1, 1], [1, 0], [0, 0]]]
var point = polylabel(polygon)

对于polygon，我们采用geojson对多边形的坐标定义格式，即多边形由多个环组成，其中第一个环是外环，其他的为内环。所以polygon[0]表示第一个环，ploygon[0][0]表示起点坐标。

准备工作

在开始实现polylabel之前，需要一些辅助函数和库。

首先，我们定义网格对象Cell：

1
2
3
4
5
6
7
function Cell(x, y, h, polygon) {
  this.x = x  // 中心点x
  this.y = y  // 中心点y
  this.h = h  // 中心点到网格的距离，相当于格网大小的1/2
  this.d = pointToPolygonDist(x, y, polygon)  // 中心点到多边形的距离
  this.max = this.d + this.h * Math.SQRT2     // 网格内部区域到多边形的最大距离
}

定义网格对象的主要目的是方便求取最大距离this.max，有了网格对象Cell之后，每当我们实例化一个cell对象，我们就可以知道这个网格区域的最大距离以及它所代表的区域。

pointToPolygonDist是计算点到多边形的距离的函数，其基本原理是计算点到多边形每条边的距离，取最短距离即为点到多边形的距离。详细的算法实现我考虑专门用一篇文章来讲。

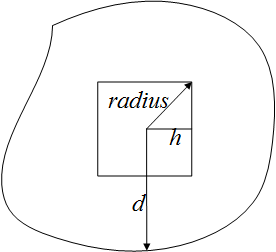
this.d + this.h * Math.SQRT2即为我们之前在算法原理中求得的最大距离dist + radius，由于格网是一个正方形，其外接圆形的半径即为中心点到任意一个顶点的距离，即this.h * Math.SQRT2。

另一个需要准备的是一个优先级队列的数据结构，它与一般的队列不同在于，优先级队列中的元素都是经过排序的。每当push一个元素，并不是简单地将该元素放入队列末尾，而是会将该元素与队列中的元素进行比较，放到一个合适的位置上。

我们可以定义一个优先级队列，队列里存储的是格网对象。每push入一个格网，根据最大距离max进行排序，大的在前，小的在后。由此，我们可以分裂格网时，只需从队首pop出一个格网进行操作。

优先级队列的一个JS实现是tinyqueue，同样是Vladimir Agafonkin的作品。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
var Queue = require('tinyqueue')

function polylabel(polygon) {

  // 计算bbox，为切分网格做准备
  var minX, minY, maxX, maxY
  for (var i = 0; i < polygon[0].length; i++) {
    var p = polygon[0][i]
    if (!i || p[0] < minX) minX = p[0]
    if (!i || p[1] < minY) minY = p[1]
    if (!i || p[0] > maxX) maxX = p[0]
    if (!i || p[1] > maxY) maxY = p[1]
  }

  // 计算长和宽，初始格网大小和高度
  var width = maxX - minX
  var height = maxY - minY
  var cellSize = Math.min(width, height)
  var h = cellSize / 2

  // 初始化一个存储Cell的优先级队列，按距离从大到小排列
  var cellQueue = new Queue(null, function(a, b) {
    return b.max - a.max
  })

  // 将多边形切分
  for (var x = minX; x < maxX; x += cellSize) {
    for (var y = minY; y < maxY; y += cellSize) {
      cellQueue.push(new Cell(x + h, y + h, h, polygon));
    }
  }

  // 取对首为最优格网
  var bestCell = cellQueue.peek()

  while (cellQueue.length) {
    var cell = cellQueue.pop()

    if (cell.d > bestCell.d) bestCell = cell

    // 最大距离小于最优格网的距离，直接淘汰
    if (cell.max <= bestCell.d) continue

    // 将格网裂为4个小格网
    h = cell.h / 2
    cellQueue.push(new Cell(cell.x - h, cell.y - h, h, polygon))
    cellQueue.push(new Cell(cell.x + h, cell.y - h, h, polygon))
    cellQueue.push(new Cell(cell.x - h, cell.y + h, h, polygon))
    cellQueue.push(new Cell(cell.x + h, cell.y + h, h, polygon))
  }

  return [bestCell.x, bestCell.y]
}

算法优化

上一节描述了多边形注记点搜寻算法的基本实现，我们还需要对其进行优化，提升算法效率。

为了提升效率，我们可以增加一个容差参数，允许最后的注记点有一定的误差，以减少运算次数:

1
2
// if (cell.max <= bestCell.d) continue
if (cell.max - bestCell.d <= precision) continue

另外，我们可以在初始时，用centroid作为初始最优点，因为大多数凸多边形的centroid就是最佳注记点：

1
2
// var bestCell = cellQueue.peek()
var bestCell = getCentroidCell(polygon)

当然，多变形的centeroid怎么求，估计又得用一篇博文来说了。

感觉给自己挖了好多坑。