求点到多边形的距离的算法实现

在之前的博文中，多边形注记点搜寻算法需要计算点到多边形的距离，本文就来讲一讲如何用JS实现点到多边形距离的计算。

如何定义点到多边形的距离？

在本文中，点到多边形的距离定义如下：

点到多边形边界的最短距离。
点在多边形内部，距离为正；在多边形外部，距离为负；在边上，距离为零。

根据上面的定义，计算点到多边形的距离需要解决两个问题：

点到多边形的最短距离如何计算？
如何判断点在多边形内部、外部、还是在边界上？

点到多边形最短距离的计算

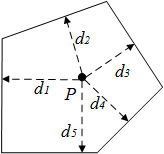
计算点到多边形最短距离的基本原理是：依次计算点到多边形每条边的距离，然后筛选出最短距离。

如下图，假设AB为多边形的一条边，现在求点P到AB的距离。

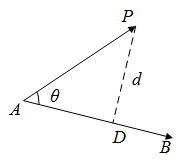
根据向量内集的公式（$\vec{a} \cdot \vec{b} = |a||b|cosθ$）,我们可以推出：
$$
\begin{align}
\vec{AB} \cdot \vec{AP} &= |AB||AP|cosθ = |AB||AD| \\
设 \quad |AD| &= t|AB| \\
则 \quad \vec{AB} \cdot \vec{AP} &= t|AB||AB| \\
t &= \frac{\vec{AB} \cdot \vec{AP}}{|AB|^2}
\end{align}
$$

根据以上公式，我们可以求出t，进而求出点D的坐标，最终PD的长度就很容易求得了。

但是还有一些边界条件需要注意，即最终D点不是落在AB上，有以下上中情况：

t < 0，D在BA延长线上，此时最短距离取PA；
0 <= t <= 1，D在AB上，此时最短距离取PD；
t > 1，D在AB延长线上，此时最短距离取PB；

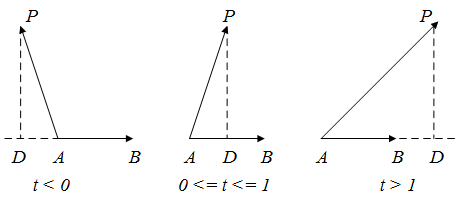
JS实现代码如下：

function pointToSegmentDist(p, a, b) {
  var AB = [b[0] - a[0], b[1] - a[1]]
  var AP = [p[0] - a[0], p[1] - a[1]]

  var AB_AP = AB[0] * AP[0] + AB[1] * AP[1]
  var distAB2 = AB[0] * AB[0] + AB[1] * AB[1]

  var D = [a[0], a[1]]
  if (distAB2 != 0) {
    var t = AB_AP / distAB2

    if (t > 1) {
      D = [b[0], b[1]]
    } else if (t > 0) {
      D = [a[0] + AB[0] * t, a[1] + AB[1] * t]
    } else {
      D = [a[0], a[1]]
    }
  }

  var AD = [p[0] - a[0], p[1] - a[1]]

  return Math.sqrt(AD[0] * AD[0] + AD[1] * AD[1])
}

判断点与多边形的位置关系

判断点与多边形的位置关系，常用的算法是射线法，即经过点沿水平方向做一条直线，观察点左边或右边交点的个数。如果交点个数为奇数，点在多变形内部；交点个数为偶数，点在多边形外部。

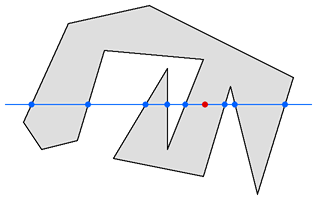
如下图，ab与过p点的水平线相交于c，则有：
$$
\frac{x_2 - x_1}{y_2 - y_1} = \frac{x’ - x_1}{y - y_1} \\
那么 x’ = \frac{(x_2 - x_1)(y - y_1)}{y_2 - y_1} + x_1
$$

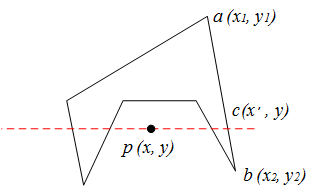
JS 算法实现为：

function pointInPolygon(p, polygon) {
  // 统计p点右边交点的个数
  var count = 0

  for (var k = 0; k < polygon.length; k++) {
    var ring = polygon[k]

    for (var i = 0; i < ring.length - 1; i++) {
      var a = ring[i]
      var b = ring[i + 1]

      if ((a[1] > y !== b[1] > y) &&
        (x < (b[0] - a[0]) * (y - a[1]) / (b[1] - a[1]) + a[0])) count++;
    }
  }

  return count % 2
}

完整实现

解决了以上两个难题之后，下面给出完整实现：

function pointToPolygonDist(p, polygon) {
  // 统计p点右边交点的个数
  var count = 0
  var minDist = Infinity

  for (var k = 0; k < polygon.length; k++) {
    var ring = polygon[k]

    for (var i = 0; i < ring.length - 1; i++) {
      var a = ring[i]
      var b = ring[i + 1]

      if ((a[1] > y !== b[1] > y) &&
        (x < (b[0] - a[0]) * (y - a[1]) / (b[1] - a[1]) + a[0])) count++;

      minDist = Math.min(minDist, pointToSegmentDist(p, a, b))
    }
  }

  if (count % 2 === 0) minDist = -minDist

  return minDist
}

Contents

如何定义点到多边形的距离？

点到多边形最短距离的计算

判断点与多边形的位置关系

完整实现