在上一篇计算多边形的最佳注记点的算法中，需要计算多边形的centroid。本文就来讲一讲多边形centroid的计算方法。

Centroid的定义

Centroid是多边形的质量中心（Center of mass）。假设多边形是一块厚度均匀的薄板，当我们用一根绳子从一个平衡点吊起薄板时，薄板能够保持水平稳定，那么这个平衡点就是centroid。

算法原理

我们先从1维直线说起，如下图，在原点的一端不同位置上分别挂着重10kg、5kg、7kg的砝码。如果我们将三个砝码当成一个整体，挂在同一个位置，使其产生的杠杆效应与之前相同，那么这个位置点就相当于质心。

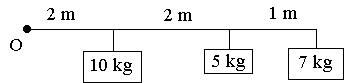
计算方法如下：

总惯性 = 10 × 2 + 5 × 4 + 7 × 5 = 75 kg.m
总质量 = 10 + 5 + 7 = 22 kg
假设质心距离原点为d，那么 22 x d = 75，得出 d = 75 / 22 ≈ 3.4 m

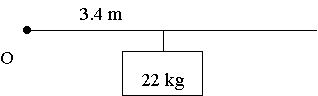
上述计算1维直线上的质心很简单，那么现在扩展到2维平面。如下图，矩形的质心很容易求得为 (2，1)。

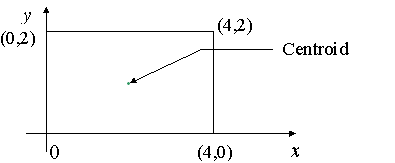
如果更复杂的形状呢？

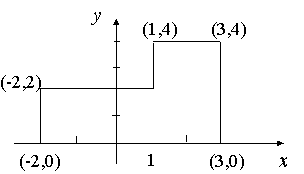
计算方法是将多边形分解为多个容易求质心的规则矩形，过程如下：

首先将多边形分解为左右两个规则矩形，如下图：

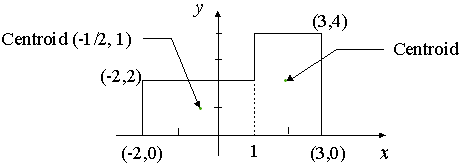
左矩形的面积为 3 x 2 = 6，质心为 (-0.5, 1)
左矩形的面积为 2 x 4 = 8，质心为 (2, 2)

我们假设多边形质量是均匀分布的，那么矩形的面积就可以代表它的质量，所以在x轴上：

1
2
3
4
6 x -0.5 + 8 x 2 = (6 + 8) x dx
-3 + 16 = 14 x dx
13 = 14 x dx
dx = 13 / 14

同理，在y轴上：

1
2
3
4
6 x 1 + 8 x 2 = (6 + 8) x dy
6 + 16 = 14 x dy
22 = 14 x dy
dy = 11 / 7

最终求得多边形的质心为(13/14, 11/7)

由以上过程，我们可以得出一个更为普遍的结论：

质心 = 惯性 / 质量

用公式表达即为：

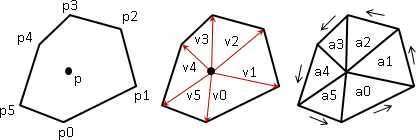
对于任意不规则多边形，如何利用上述公式计算质心呢？其原理是将多边形剖分为三角形，然后分别计算每个三角形的面积和质心。

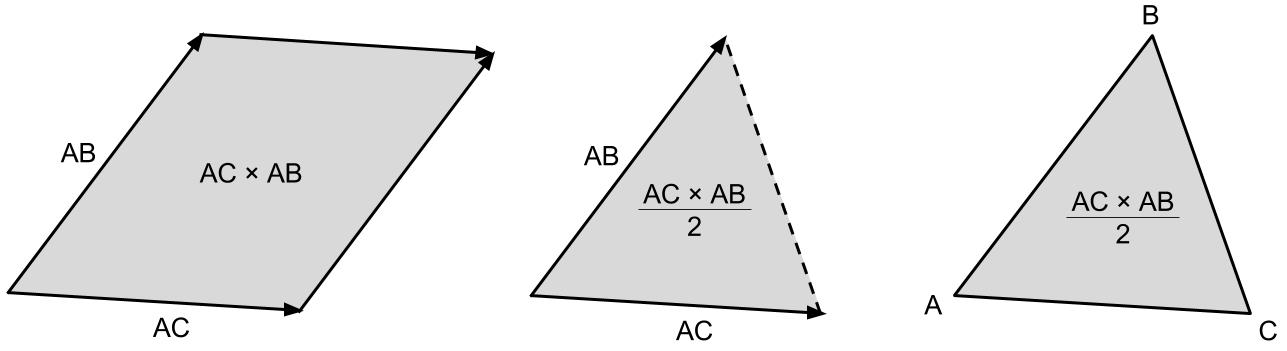
对于三角形的面积，我们可以采用向量积公式计算:
$$
signedArea(ABC)=\frac{1}{2}(x_1y_2 - x_2y_1)
$$

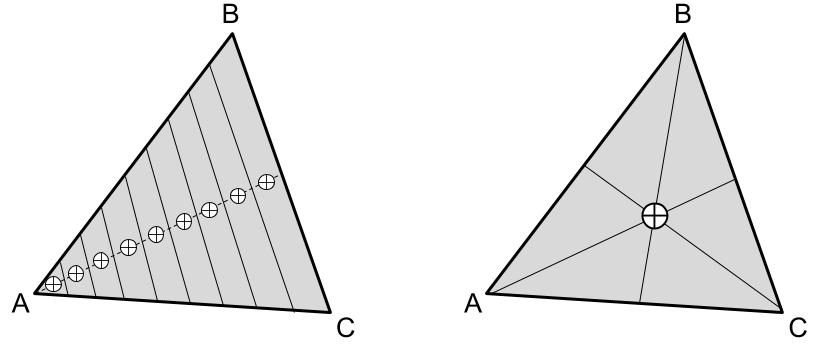
对于三角形的质心，采用如下公式计算：
$$
centroid(ABC)=(\frac{A_x + B_x + C_x}{3}, \frac{A_y + B_y + C_y}{3})
$$

剩下的任务是选择一个剖分点P，将多边形剖分为多个三角形。由于我们在用向量积计算三角形面积时，其结果是有正负的。选择哪一个剖分点，并不影响最终加和后的总面积，前提是多边形的坐标点按逆时针排列。所以，为了简便期间，选取坐标原点作为剖分点。

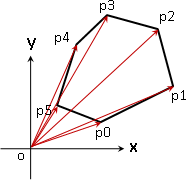
具体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// polygon按顺时针排列顶点
function getCentroid(polygon) {
  var totalArea = 0
  var totalX = 0
  var totalY = 0
  var points = polygon[0]

  for (var i = 0; i < points.length; ++i) {
    // a、b以及原点构成一个三角形
    var a = points[i + 1]
    var b = points[i]

    var area = 0.5 * (a[0] * b[1] - b[0] * a[1])  // 计算面积
    var x = (a[0] + b[0]) / 3  // 计算x方向质心
    var y = (a[1] + b[1]) / 3  // 计算y方向质心

    totalArea += area
    totalX += area * x
    totalY += area * y
  }

  return [totalX / totalArea, totalY/ totalArea]
}